- 키를 안전하게 공유하지 않고 그냥 보낸다면 (telnet)
- 공격자가 도청했을 때 그 키로 메세지를 풀 수 있다 → 이후에 암호화 해도 소용 X
- 대칭키를 사전에 공유해야 하는데..
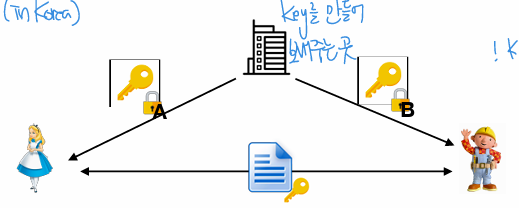
- 키를 안전하게 보내는 방법
- 키의 사전 공유에 의한 해결
- 키 배포 센터(Key Distribution Center, KDC)에 의한 해결 : 믿을 수 있는 제 3자와 미리 공유한 key가 있어야 함
- Diffie-Hellman 키 교환
- 공개 키 암호에 의한 해결
- 쌍방이 사전에 공유해놓은 키를 이용해 새로운 키를 공유하는 방식
- 데이터 통로가 만들어지는 격
- Enigma, CDMA가 채택하는 방식
- 문제점
- 준비해야 하는 사전 공유 키의 수가 폭발적으로 늘어남

- 사전 공유 키를 어떻게 공유할지 → 실제로 만나서 공유하는 것이 best
- 사전 공유키가 노출되면 다시 공유해야 함
- 연결 요청 메세지를 KDC에 전송
- KDC, Alice 사이에는 사전 공유된 키 존재
- KDC, Bob 사이에도 사전 공유된 키 존재
- KDC가 연결 요청을 받으면 일회용 세션키 생성
- 세션키를 Alice와 공유하고 있던 키로 암호화 한 다음 Alice에게 전송
- 세션키를 Bob과 공유하고 있던 키로 암호화 한 다음 Bob에게 전송
- Alice와 Bob은 논리적 연결 가능 (통신 O)
- 세션 키를 이용해 데이터를 암호화하여 전송
- 문제점 : KDC 부하 증가, KDC가 공격 타겟이 됨, KDC의 신뢰성 문제
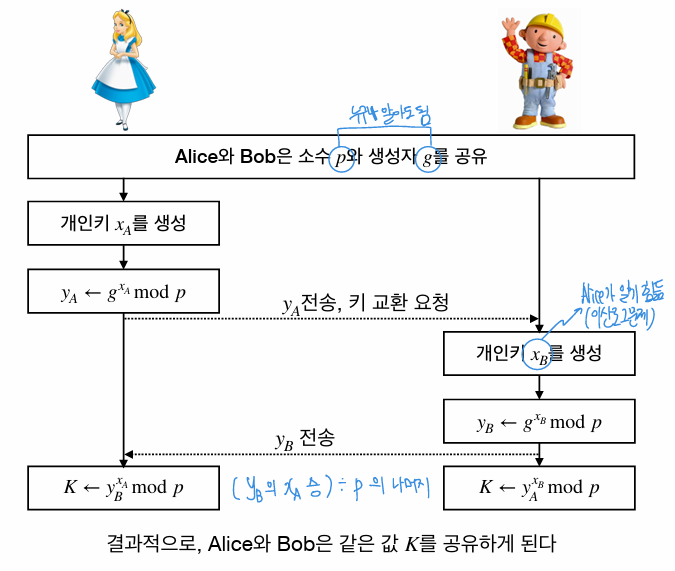
- 두 사용자가 데이터 암호화에 사용될 대칭키를 공유하기 위한 알고리즘
- 중간에 Alice와 Bob이 교환하는 값들을 도청해도 대칭키를 알아내는 것은 불가능
- 이산 로그 문제를 푸는 것이 매우 어렵다는 데에 근거
- 이산 로그 문제 (discrete logarithms problem)

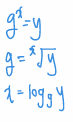
- 정의
- 공개값 : g (생성자), p (매우 큰 소수)
- 비밀키 : x
- 공개키 : y = g^x mod p (g^x / p 의 나머지)
- 생성자 g가 만족해야 할 조건


- 잉여 관련
- 모듈로 7이다 = 세상에 숫자는 0~7 = 나머지 숫자는 매치
- 3개의 정수 a, b, n에 대해 a-b가 n의 배수일 때 다음과 같은 합동식을 쓴다
- a ≡ b ( mod n)
- module로 합동이다, 법 n에 대해 합동이다
- Ex. 4 ≡ 16 (mod 6), -3 ≡ 22 (mod 5), 4 !≡ 19 (mod 7)
- 기본적인 성질
- gcd (c, m) = 1 : c와 m의 최대공약수가 1이다

Background - Fermat's Little Theorem
- 소수 p에 대해 p의 배수가 아닌 정수에 p-1 거듭제곱을 하면 1이 된다 (또는 p로 나눈 나머지가 1이 된다)
- 거듭제곱 / p 의 나머지는 1 ~ p-1 중 하나인데 언젠가는 1도 등장한다 → 그럼 그때부터 순환 → 그 순환주기를 나타낸 것이 페르마의 작은 정리

Bakground - 원시근 (Primitive Root)

- Ex. p = 13 일 때, 2, 6, 7, 11은 원시근이지만 그 외의 수들은 원시근이 아니다

- 소수 p가 주어졌을 때, g는 원시근 중 하나로 정하여 사용한다
- 생성자 고르기
- 비밀키는 서로 다른데 공개키는 같은 문제 발생을 막기 위해 원시근을 써야 한다
- Alice는 Xa = 97, Bob은 Xb = 233을 선택했다고 가정 (비밀키이므로 서로 몰라야 함)
- Alice와 Bob은 다음과 같이 공개키를 계산
- Ya = 3^97 mod 353 = 40
- Yb = 3^233 mod 353 = 248
- 40과 248은 공개 키
- Alice와 Bob은 서로 공개 키 교환
- Alice와 Bob은 다음과 같이 공유키 K 계산
- Alice : 248 ^ 97 mod 353 = 160
- Bob : 40 ^ 233 mod 353 = 160
- Alice과 Bob이 같은 킬르 갖게 되는 이유

- 보안성
- 키 교환 과정에서 공격자가 알 수 있는 정보는 p, g, Ya, Yb
- K를 계산하기 위해서는 Xa나 Xb 중 적어도 하나를 알아야 함
- 현재 주어진 정보만으로 비밀키를 구하는 것은 이산 로그 문제로 매우 어렵다 (Ya = g^Xa mod p) → 거의 불가능
- 프로토콜의 허점을 이용한 공격에는 약하다
- 수행 시간
- Xa 를 찾는 것이 어려운데 n bit일 때 다 대입해 알아내야 한다면 O(p)만큼 걸린다
- O(p) = O(2^n), O(p^1/2)까지 가능




중간자 공격 (Man-in-the-Middle)
- 통신에 참여하는 쌍방의 사이에서 공격을 일으키는 행위
- Diffie-Hellman 키 교환 기법은 중간자 공격에 매우 취약함
- 공격자(Darth)의 목표
- Alice와 Darth의 공유 키 생성
- Bob과 Darth의 공유 키 생성
- 이때 Dart의 존재는 둘 다 모름
- Darth가 일으킬 수 있는 공격
- 메세지를 엿보는 해우이
- 한쪽이 보낸 메세지를 다른쪽으로 보내지 않는 행위
- 한쪽이 보낸 메세지를 변경하여 다른쪽으로 보내는 행위
- 메세지를 임의로 생성하여 Alice 또는 Bob에게 전송

- 공개 키
- for 데이터 암호화
- 문제점 : 느리고 모두 암호화 X
- 공개 키 암호
- 키 분배 문제 해결 가능
- 대칭 키 생성 후 공유할 때 사용
- 현재 가장 많이 사용
- 공개 키 암호 기반의 키 분배 과정
- 공개 키의 분배
- 공개 키 암호를 이용한 대칭 키 분배
- 공개 키 주인을 인증해야 하는 문제가 발생할 수 있음 → 추가적인 보안/인증 기술로 해결
- 과정
- Alice가 세션 키 랜덤 생성
- Bob이 사전에 공개 키를 전파, 비밀 키도 소유
- Alice→Bob : 세션 키를 공개 키로 암호화
- Bob이 개인 키로 세션 키 복호화
- 세션 키 공유 가능

- 1976년 Diffie와 Hellman이라는 사람들에 의해 처음 제안
- 대칭키 암호와는 달리 비트 연산이 아닌 정수론적 지식을 기반으로 함
- 대칭키 암호와는 달리 암호화에 쓰이는 키와 복호화에 쓰이는 키가 서로 다름
- 비대칭 key라고도 부름
- 오해
- 공개키 암호가 대칭키 암호보다 더 안전하다
- 실제로 AES 256과 RSA 1024가 보안 수준이 비슷
- 그러나 필요한 키의 크기는 RSA가 4배로 더 큼
- AES 256 >> RSA 256
- 공개키 암호는 대칭키 암호를 완전히 대체할 수 있다
- 같은 크기의 평문을 암호화 하는 데에 있어서 공개키 암호가 연산량이 훨씬 많음
- 속도 : AES 1024 >> RSA 1024
- 데이터 암호에는 대칭키 암호가 사용됨
- 공개키 암호는 대칭키 공유 이슈를 해결
- 공개키 암호 : 큰 데이터 암호화에는 부적절, 작은 데이터 (세션키) 암호화에 적절
- 공개키를 사용하면 키 공유 이슈가 해결된다
- 대칭키 암호의 키 공유 이슈 해결
- 인증과 관련된 이슈가 남음
- 추가적인 프로토콜(인증서) 필요
- 공개키와 대칭키는 상호보완적
- 공개키 for 세션키 암호화
- 대칭키 for 데이터 암호화
- Alice가 비밀키를 임의로 생성하고 그의 짝이 되는 공개키를 계산해냄
- Alice가 공개키를 공개 (앞으로 나한테 보낼 때는 이걸로 암호화 해서 보내!)
- Bob이 Alice에게 메세지를 보낼 때 공개키로 암호화
- Alice가 Bob으로부터 암호화된 메세지를 받으면 자신의 비밀키로 복호화
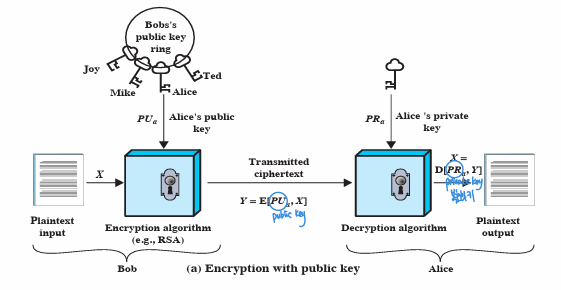
- 주로 메세지 암호화
- 메세지 발신자를 증명하는 데에도 사용
- Bob이 비밀키를 생성하고 그의 짝이 되는 공개키를 계산
- Bob이 공개키를 공개
- Bob이 Alice에게 보낼 메세지를 자신의 비밀키로 암호화하고 메세지 원본과 비밀키로 암호화된 버전을 Alice에게 보냄
- Alice는 Bob의 공개키로 암호화된 메세지를 복호화하고 메세지 원본과 대조
- 기밀 달성 목적 X, 무결성 달성 목적
- 비밀키로 암호화 → 사인은 본인만 할 수 있어야 하니까
- 공개키로 암호화된 메세지 복호화 → 검증은 아무나 할 수 있어야 하니까
- 착한 사람 입장
- 키의 주인은 비밀키와 그에 대응되는 공개키를 계산하는 것이 매우 쉬워야 함
- 메세지를 공개키로 암호화하는 것은 계산적으로 쉬워야 함
- 암호화된 메세지를 비밀키로 복호화하는 것은 계산적으로 쉬워야 함
- 나쁜 사람 입장
- 공개키로 암호화된 메세지를 비밀키 모르는 상태에서 알아내는 것은 계산적으로 거의 불가능해야 함
- 공개키만을 알고 있는 상태에서 비밀키를 알아내는 것은 계산적으로 거의 불가능해야 함
- Encryption = Cryptograph = 암호
- Encrytion은 데이터 기밀성을 위한 것
- Cryptograph는 데이터 보안을 위한 것
- Encryption ⊂ Cryptograph
- 현재 많이 사용되는 공개키 암호(Cryptograph) 시스템 기반 알고리즘

- 정수론 지식을 이용한 암/복호화 기법
- 키 생성 : 유큘리드 알고리즘 (최대공약수, 부정방정식 해 구하기)
- 암/복호화 : 오일러 정리 (페르마의 작은 정리의 일반화)
- 가장 대표적인 비대칭키 방식
- 매우 큰 자연수의 소인수분해가 어려움을 이용
- 세션키 암호화, 전자서명에 사용
- 공인인증서, 공인인증기관 서명, htttps
- 랜섬웨어 (세션키와 내용 모두 암호화)
- 두 자연수의 최대공약수를 구한느 알고리즘
- 계산 과정
- a에서 b를 나눈 몫을 q, 나머지를 r이라 한다
- r = 0 이면 b가 최대공약수가 되고 알고리즘을 끝낸다
- 만일 r ≠ 0 이면 b → a에 대입, r → b에 대입하고 1번으로 돌아가 반복한다
- Ex. 2021과 917의 최대공약수 구하기

- 두 개의 정수 A, B와 d = gcd(A,B)에 대해 다음 부정방정식의 정수해를 찾는 과정
- Ax + By = d
- 해가 무조건 있으며 그것을 구하는 것이 유클리드 알고리즘
- 유클리드 호제법의 과정을 거꾸로 거슬러 올라가면 됨
- Ex

- 공개키와 비밀키 쌍 생성을 위해 사용됨
- 3개의 정수 a, v, n에 대해 a x v ≡ 1 (mod n) 일 때 a와 v를 법(modulo) n에 대한 잉여 역수라고 함
- 또는 v는 a의 법 n에서 곱셈에 대한 역원이라고도 함
- Ex
- 3과 2는 법 5에 대한 잉여 역수 → 이 세상의 수가 0,1,2,3,4만
- 12와 10은 법 17에 대한 이여 역수 → 12와 17, 10과 17이 서로소이면 잉여 역수 O
- 12의 법 15에 대한 잉여역수는 존재하지 않을 수 있다 → 12가 3의 배수이기 때문에, 12x = 15k + 1 이 성립하려면/15로 나누었을 때 1이 남으려면 12가 3의 배수이면 안됨
- 문제
- 7의 법 16에 대한 잉여역수를 구하세요
- 7 * x ≡ 1 (mod 16) → x = ?
- 7x = 16k+1
- x = 7, 49 = 48+1 (k = 3)
- 917의 법 2021에 대한 잉여역수를 구하세요
- 917 * x ≡ 1 (mod 2021) → x = ?
- 917x = 2021k + 1
- 917x - 2021k = 1 → 구하기 어려움
- 수가 커지면 반복 대입으로 잉여역수를 구하기 매우 어려워짐
- 이때 유클리드 알고리즘 사용
- 일반적으로 a의 법 n에 대한 잉여 역수 구하기 (a와 n은 서로소)
- ax + ny = 1 의 정수해 순서쌍 (x,y) 하나를 구한다 → 유클리드 사용
- 917x + 2021k = 1 → (x,k) = (-562,255) = (1459, -662) → mod 2021에서는 동일한 숫자
- x가 바로 a의 잉여 역수
- 자연수 n에 대해 n 이하의 n과 서로소인 자연수의 개수를 ∮(n)이라고 한다
- Ex
- ∮(10) = 4 → 1,3,7,9
- ∮(25) = 20 → 5,10,15,20,25 제외 전부
- ∮(32) = 16 → 2의 배수 전부 제외
- ∮(91) = 72 → 7,13의 배수 전부 제외
- n = p x q 꼴 (단 p,q는 소수)일 때 ∮(n) = (p-1)(q-1)
- n과 서로소가 아닌 수는 p의 배수이거나 q의 배수인 수
- n 이하의 p의 배수는 q개, q의 배수는 p개, p와 q의 공배수는 1개


- 서로 다른 두 소수 p, q에 대해 n = p x q 로 정한다
- 공개키를 e, 비밀키를 d라 할 때, e와 d는 다음 합동식을 만족하게 결정한다
- e x d = 1 (mod ∮(n))
- 잉여역수 관계
- e x d = ( ∮(n)의 자연수배 + 1)
- n 이하의 자연수 M은 다음 식을 만족

- 공개되는 값 : e, n
- 비밀값 : d, p, q, ∮(n)
- e, d는 ∮(n)와 서로소여야 함 → 그래야 잉여 역수 O
- 메세지는 n과 서로소여야 함
- RSA 단점 : 모든 메세지를 암호화 X, 메세지가 p혹은q의 배수이면 X
사진 참조- 과정
- Alice가 자신에게 전송하는 데이터를 모두 암호화 한다고 가정
- Alice는 매우 큰 서로 다른 두 소수 p와 q를 선택
- n ← pq, ∮(n) = (p-1)(q-1) 계산
- ∮(n)과 서로소인 정수 e 선택
- ed ≡ 1 (mod ∮(n) )인 정수 d를 계산 (유클리드 알고리즘 사용)
- 공개키 {e, n} 배포 ( ∮(n)과 e, d는 서로소여야 함)
- Bob이 Alice에게 메세지 M을 보내기 위해 다음 수행
- C ← M^e mod n 을 계산
- Bob이 Alice에게 C 값을 전달
- Alice는 C^d mod n 하여 M을 알아냄
사진 참조
- 공격자의 목표
- e와 n이 주어졌을 때 비밀키 d(∮(n)의 잉여역수)를 알아내는 것
- ed ≡ 1 (mod ∮(n))인 정수 d를 알아내려면 ∮(n)을 계산할 수 있어야 함
- ∮(n) = (p-1)(q-1)이므로 p와 q를 알아내야 하는데 이를 위해 n을 소인수분해 해야 함
- n을 얼마나 소인수분해하기 어려운지가 RSA의 보안성을 결정하는 요소
- 소인수분해를 어렵게 하기 위해서는 p와 q가 매우 커야 하며 동시에 두 소수의 차도 매우 커야 함
- 현재까지는 안전한 RSA를 위해 2048비트의 n을 권장
- 타이밍 공격
- 복호화 알고리즘 실행시간을 관측하여 비밀키의 길이를 예측하는 공격 (d를 예측)
- 방어방법 : 랜던 지체 (복호화 시간을 지연시킴, 복호화 하자마자 값을 내놓게 X)
- 선택 암호문 공격 (Chosen-Ciphertext Attack)
공격자가 해볼만한 것방어방법 : 평문에 패딩 추가최적 비대칭 암호화 패딩(OAEP) 활용



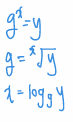





















![[CS][알기 쉬운 정보보호개론 3판] Chapter06. 공개키 암호](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FwjGkY%2FbtsyEz12kAS%2FjJcsAmKUSQKZKhNgaVC2Sk%2Fimg.png)