[CS][알기 쉬운 정보보호개론 3판] Chapter08. 일방향 해시함수

 

 

 

데이터의 무결성

• 데이터가 함부로 위/변조 되지 않았다는 것을 증명
• 무결성 검사를 위한 방법으로 다른 안전한 장소에 복사본을 저장하는 방법이 있다 → 공간 낭비의 문제점
• 파일로부터 나올 수 있는 작은 값을 보관하기 → 해시값,지문,Message Digest
  • 이러한 값을 만들어내는 함수를 해시 함수라 한다.

 

 

 

해시 함수

• 함수 H(x)가 x가 임의의 길이라도 함숫값의 길이는 항상 일정할 때
• 해시값의 길이는 메세지의 길이와는 관계 X
• 입력값은 모든 디지털 데이터가 가능 (임의+값X 것까지)

 

 

 

해시 함수와 안전한 해시 함수

• 만족해야 하는 성질
  • 임의 크기의 데이터 블록에 적용
  • 일정한 길이의 출력
  • 계산 용이성과 구현 가능성
• 해시 함수가 ‘안전하다’ 라고 말할 수 있는 성질
  • 비가역성 : 한 방향으로만 계산, 역함수X, H(x)=y일 때 y가 되게 하는 x를 찾는 것이 어려움
  • 약한 충돌 저항성
  • 강한 충돌 저항성
• 해시 함수가 많이 쓰이는 이유
  • 무결성을 위해 많이 쓰임
  • 원본 데이터를 몰라도 매우 작은 사이즈만으로도 원본이 변경되었는지 알 수 있음
• 주요 용도
  • 메세지 무결성 인증
  • 디지털 서명

 

 

 

비가역성

• 주어진 값 h에 대해 H(x) = h가 되게 하는 x를 찾는 것이 계산적으로 불가능
• 하나의 비트만 달라도 해시값이 완전히 달라져야 함
• 프리이미지 저항성

글로 표현하기 어렵다는 판단에.. 손필기를 첨부합니다.

 

 

 

충돌 저항성

• 공통점 : 충돌을 막음
• 차이점 : 주어지는 것이 다름
• 약한 충돌 저항성
  • 주어진 x에 대해 H(x)=H(y), x≠y를 만족하는 y를 찾는 것이 매우 어렵다
  • 주어진 메세지의 해시값과 동일한 해시값을 갖는 다른 메세지를 만드는 것이 불가능
  • 2차 프리이미지 저항성
  • M1을 주고 M2 찾는 것이 어려워야 함
• 강한 충돌 저항성
  • H(x)=H(y), x≠y를 만족하는 x,y을 찾는 것이 매우 어렵다
  • 해시 값이 일치할 것 같은 서로 다른 두 개의 메세지를 발견해 내는 것이 불가능
  • Birthday Attack을 방지기 위한 조건
  • 처음부터 M1, M2 찾는 것이 어려워야 함

 

 

 

해시함수 관련 용어

• 일방향 해시 함수
  • Message Digest Function
  • Cryptographic Hash Function
• 일방향 해시 함수의 입력값
  • 프리 이미지
• 해시값
  • 메세지 다이제스트
  • 핑거프린트
• 무결성
  • 완전성
  • 보전성

 

 

 

해시함수의 사용 예시

• 암호화 키를 만들 때도 사용됨
• 소프트웨어 변경 검출 : App store와 자동차
• Password-based Encryption : PW 가지고 암호화
• 메세지 인증 코드 : msg를 보낸 사람과 변했는지 안변했는지
• 디지털 서명 : 누구나 검증 가능
  • 공통점 : 무결성을 위해, 누가 보냈는지 확인
  • 차이점 : MAC - 키를 가지는 사람만 검증 가능, 서명 - 누구나 검증 가능
• 의사 난수 생성기
• 일회용 비밀번호 : OTP

 

 

 

일방향 해시함수의 종류

• MD4
  • Rivest가 1990년에 만든 해시 함수로, 128비트의 해시 값을 반환
  • Dobbertin에 의해 충돌 방법이 고안되어, 현재는 사용되지 않는다
• MD5
  • Rivest가 1991년에 만든 해시 함수로, 역시 128비트의 해시 값을 반환
  • 여러 가지 공격 방법들이 개발되었지만, 완전히 뚫린 것은 아니긴 하다. 그래도 현재는 사용을 권장하지 않는다.
• SHA-1
  • 1995년에 기존 SHA의 보안 문제점을 보완하기 위하여 수정된 버전
  • 기존 SHA와 구분하기 위하여 첫 번째 버전을 SHA-0라 부른다
  • 해시값의 길이는 160비트
• SHA-2
  • 2001년에 SHA-1의 문제점을 해결하기 위하여 수정된 버전
  • 해시값의 길이로 224, 256, 384, 512비트가 가
  • 각각을 SHA-224, SHA-256, SHA-384, SHA-512 라고 부른다
  • 전체 입력 데이터를 메모리에 저장해서 처리할 필요 없이 도착하는 블록마다 처리할 수 있으므로 온라인에서 사용이 적합
• SHA-3
  • 현재까지 나온 해시 알고리즘 중 가장 안전하다고 알려진 버전
  • SHA-2를 완벽하게 대체할 수 있어야 하므로, SHA-2의 특징은 모두 갖고 있으면서 보안성이 강화
  • 해시값의 길이는 사용자가 원하는대로 정할 수 있다

 

 

 

SHA-3

• 현재 해시 함수의 표준
• KECCAK이 최종적으로 선정
  • SHA-2와 다른 구조, 구조가 투명하여 해석하기 쉬움
  • 다양한 디바이스에서 구동되고 조합 형태로도 양호
  • 하드웨어 상에 내장 시에 높은 고성능을 낼 수 있음
  • 스펀지 구조

 

 

 

해시함수에 대한 가능한 공격 - 전사공격

• 약한 충돌 저항성을 깨고자 하는 노력
  • 충돌은 일어날 수 밖에 없지만 지극히 적어야 한다
  • 공격자 입장에서는 충돌 일으키기가 어려워야 한다

 

 

 

해시 함수에 대한 가능한 공격 - Birthday Attack

• 강한 충돌 저항성을 깨기 위한 공격
• N명 중에서 생일이 같은 사람이 존재할 확률이 1/2 이상이 되기 위한 N의 최솟값은? 
• 해시함수에서는 H(x)=H(y)인 서로 다른 x,y를 찾는 공격이다.

 

 

 

전사공격과 Birthday Attack의 공격/방어 난이도

• 해시함수의 공역의 원소의 개수를 N이라 할 때

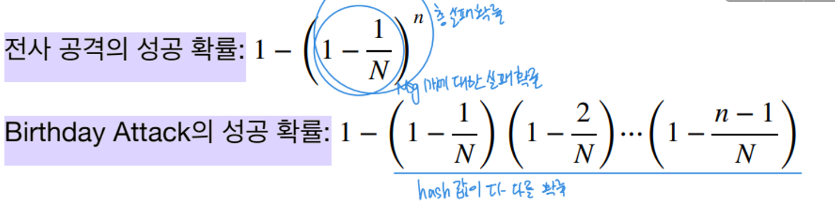
• 위의 두 확률 중 Birthday Attack의 성공 확률이 더 크다.
• 공격 난이도는 Birth attack이 더 쉽다. 방어하는 측에서는 Birthday Attack의 방어가 더 어렵다.

 

 

 

해시함수의 한계

• 거짓 행세 검출은 못한다
• 처음부터 잘못된 메세지가 저장되게 되면 알아챌 수 없다
• 메세지 인증 코드와 디지털 서명으로 처음부터 저장할 때 검사 필요